Stereo Visual Odometry C++ implementation!
on Self-study
이번 글은 지난 포스트에 이어서 Stereo Visual Odometry에 대한 포스트이다. 이번 글에서는 Stereo Visual Odometry의 C++ implementation에 대해서 간략하게 설명한다. 코드는 ORB-SLAM2에서 사용한 ORB feature 기반의 Stereo matching 기법과 GTSAM의 projection BA (Bundle adjustment)를 이용해서 작성하였다. Odometry dataset은 public dataset인 Kitti Odometry Benchmark를 사용하였다.
Stereo Matching
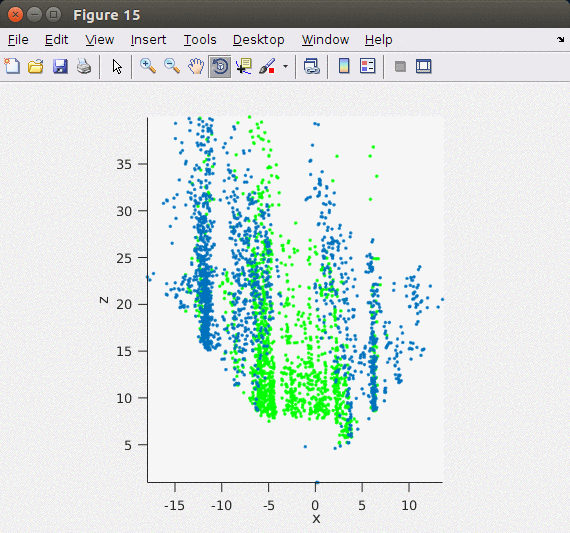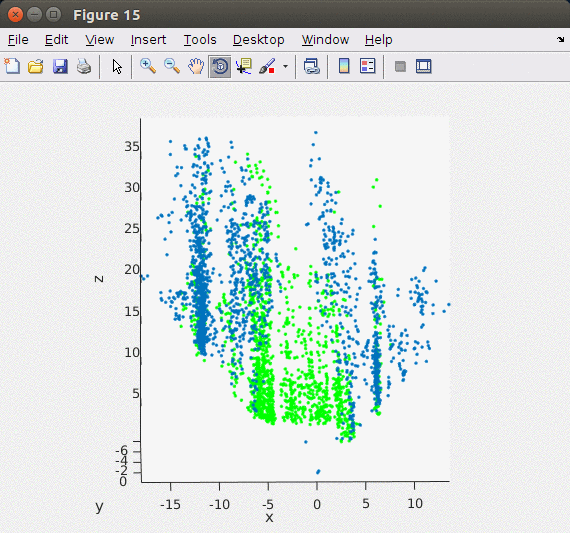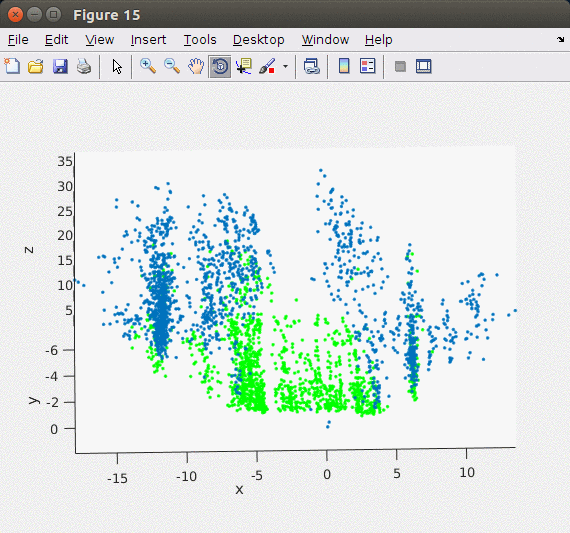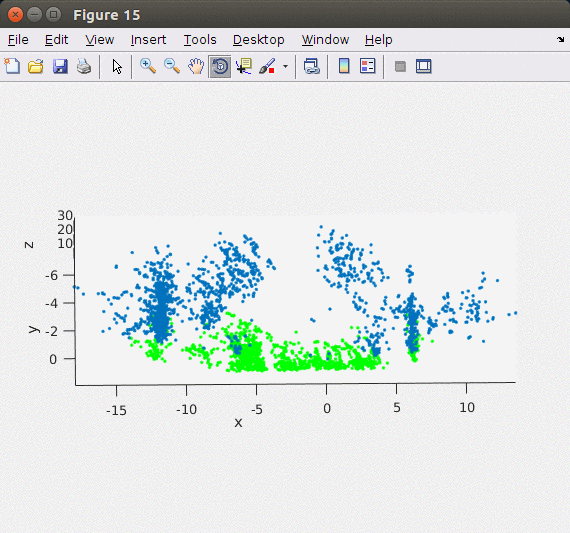
지난 Stereo Odometry의 Matlab 기반 포스트와는 달리 이번 글에서는 ORB feature를 이용해서 포인트 기반으로 빠르고 안정적으로 stereo matching을 할 수 있는 ORB SLAM2의 방법을 차용하여 구현하였다. ORB SLAM2에서는 왼쪽, 오른쪽 이미지에서 각각 ORB feature/descriptor를 추출한 후 왼쪽 이미지와 가장 matching이 잘 되는 오른쪽 이미지의 descriptor를 matching 포인트로 이용하였다. 엄밀하게 매칭 포인트를 구하기 위해서 feature description의 각 Octave level에서 matching을 해서 disparity를 구한다. 아래의 이미지가 Stereo Matching에서 구한 feature를 3차원 포인트로 복원한 모습으로 지면 영역 (초록색 포인트)과 옆 건물들(파란색 포인트)이 제대로 표현된 것을 확인할 수 있다.
Motion estimation
이전 프레임의 왼쪽 이미지 I^{t-1}_l과 현재 프레임의 왼쪽 이미지 I^{t}_l가 모션을 구하기 위한 포인트로 사용된다. ORB descriptor가 Binary descriptor이기 때문에 Opencv에서 Brute-Force Hamming Distance를 Matching Distance로 사용하고 Nearest Neighbor Distance Ratio (NNDR)을 이용해서 두 프레임간의 매칭 포인트를 구한다. 아래의 과정은 두 프레임간 매칭포인트를 구한 후 Outlier를 제거하고 Inlier와 대응되는 3차원 포인트 (스테레오 카메라이므로)를 이용해서 모션을 구하는 방법이다.
Compute Inliers
모션을 구하기 위해 Bundle adjustment를 하기 전 해야하는 과정은 바로 Feature matching과 Outlier를 최대한 제거하는 과정이다. 물론 Bundle adjustment (BA)를 하기위해서 error model을 세울 때 robust kernel을 이용해서 (Huber weight와 같은 M-estimator) Outlier의 영향을 줄일 수 있지만 기본적으로 모든 포인트의 에러를 줄이는 방향으로 최적화가 되기 때문에 Outlier가 모션 추정에 영향을 주는 것이 사실이다. 이러한 문제를 방지하기 위해 많이 사용하는 방법이 Motion Model을 기반으로 한 (Homography나 Fundamental Matrix) RANSAC 알고리즘을 이용해서 Inlier를 추리는 방법이다. RANSAC은 어떤 모델의 파라미터를 구하기 위한 포인트 N개를 랜덤하게 뽑고 모델에 적용했을 때의 포인트들의 에러를 구해서 일정 에러 이내의 포인트를 추리고, 다시 랜덤하게 뽑고 하는 과정을 통해서 모델을 구하는 방법이며 링크된 블로그에 자세한 설명이 되어있다. C++ 코드를 작성하는 경우에는 opencv를 이용하면 매우 간편하게 homography나 fundamental matrix기반의 RANSAC을 적용할 수 있다. 아래의 코드에서 points1, points2가 의미하는게 연속된 두 프레임에서 매칭된 ORB feature들이며 status가 각 포인트가 Inlier인지 Outlier인지 나타내는 Index가 CV::Mat의 type으로 저장되어있다.
// Fundamental matrix
H = cv::findFundamentalMat(points1, points2, cv::FM_RANSAC, error, 0.99, status);
// Homography
H = cv::findHomography(points1, points2, cv::RANSAC, error, status);
위 설명과 같이 Fundamental Matrix (또는 Essential Matrix)나 Homography 기반의 RANSAC을 수행한 후 연속된 왼쪽 프레임 간의 Inlier를 그려보면 아래의 그림과 같이 나타나는 것을 확인할 수 있다. 육안으로 확인해 보면 대부분 잘 매칭된 (Cross 되어 연결된 선들이 보이지 않기 때문에) 결과를 나타낸다.

Two-view BA
위 과정에서 Inlier point를 추리고 나면 이제 연속된 프레임에서 어느정도 신뢰할 만한 매칭 포인트를 가지고 있다고 말할 수 있다. 이제 이 포인트들을 이용해서 두 카메라간의 모션을 구하는 방법에 대해서 살펴본다. 이 방법은 ORB-SLAM2에서 Appendix의 Bundle adjustment와 같은 방법으로 multi-frame에 대해서 적용할 수 있지만 이번 구현에서는 연속된 영상의 two-view BA에 적용하였다. 우선 방법에 대해서 간단히 말로 풀어쓰면 다음과 같다. 기준 프레임 (이전 프레임)에서 포인트들의 초기 3차원 위치를 알고 있을 때 이 포인트들을 임의의 모션을 이용해 타켁 프레임으로 transform하고 이미지 좌표계 상으로 projection 했을 때의 포인트 위치 (u, v)는 feature matching에서 구한 대응되는 feature들의 위치와 같아야 한다. 우선 i번째 포인트의 이미지 좌표상의 위치와 \mathbf{x} = (u, v)와 3차원 위치 X = (x, y, z)를 식과 같이 표현하며 아래의 subscription은 해당하는 프레임을 의미한다. 프레임간의 모션은 \mathbf{T}_{t-1,t}로 나타냈으며 의미는 t-1에서 t로의 모션을 뜻s한다. 아래의 식은 포인트 i에 대한 에러를 나타내며 \pi는 3차원 포인트를 이미지 상으로 projection하는 projection function을 의미한다.
\mathbf{e}^i = \mathbf{x}^i_{t}-\pi^i(\mathbf{T}_{t-1,t}, X^i_{t-1})그러므로 Cost function은 위 에러의 합이 최소화 되는 방향으로 최적화 되며 아래의 식과 같이 표현할 수 있다. 아래의 식에서 \Omega는 2x2 Covariance matrix이며 \rho는 robust kernel인 M-estimator를 의미한다. 본 구현에서는 Huber cost function을 적용하였다.
C=\sum_{i}\rho(\mathbf{e}^i\Omega^{-1}\mathbf{e}^i)실제로 Motion을 구하기 위해서는 Cost function에서 Error term을 현재 motion에 대해서 Linearize하고 Jocobian을 구해서 motion을 delta만큼 업데이트 하는 과정을 반복해서 수행하야한다. 즉, 함수최적화에서 Nonlinear Least Square 문제를 푸는 것과 같다. 일반적인 함수최적화 문제에서 모델 파라미터가 모션 정보로 볼 수 있다. Nonlinear least square 문제는 여러가지 방법으로 풀 수 있는데 SLAM에서 주로 사용하는 방법은 Gauss-Newton이나 Levenberg-Marquardt을 들 수 있다. 또한 이미 많은 오픈소스 Back-end library등이 공개 되어 있는데, 그 중 유명한 것은 ISAM, G2O, 그리고 GTSAM이 있다. 이번 포스트에서는 이 중 GTSAM을 사용하여 코드를 구현하였다! (이러한 경우 실제 파라미터 업데이트는 라이브러리에서 구현되어 있으므로 사용자는 measurement 정의만 잘 해주면 쉽게 모션을 구할 수 있다.)
Result and Conclusion
다음은 Two-view BA를 통해서 구한 frame간 Relative Pose를 Compose 하여 Vehicle Trajectory를 구한 결과이다. Initial frame을 (0, 0, 0)로 하여 Compose를 하면 i번째 frame의 Vehicle Pose는 \mathbf{T}_{0,i}=\mathbf{T}_{0,1}\mathbf{T}_{1,2} \cdots \mathbf{T}_{i-2,i-1}\mathbf{T}_{i-1,i} 이 식과 같은 Motion composition을 통해서 구할 수 있다. Test는 KITTI odometry benchmark dataset에서 00번과 06번 시퀀스에서 진행하였다. Odometry benchmark의 Ground truth와 같이 깔끔하게 Path가 나오진 않았지만 Rotation에서 부분적으로 Bias가 나온 것을 제외하고는, 그리기 Loop closure, Keyframe없이 단순히 Two-view만 이어 붙인 것 치고는 생각보다는 준수한 결과가 나온것을 확인할 수 있다.
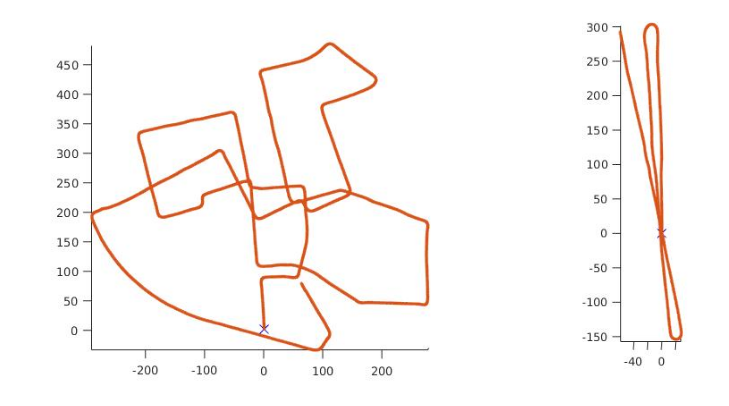
사실 어찌보면 KITTI dataset은 사용하기가 매우 편리하고 (Sync, Distortion, Rectification이 이미 되어있는!!) 영상도 깔끔하기 때문에 위와 같이 큰 추가사항들 없이 결과를 뽑아도 꽤 괜찮게 나오긴 했다. 하지만 실제로 데이터를 획득해서 돌려보면 생각보다 데이터 전처리가 많이 들어가야 하고, 생각보다 다른 외적인 요인들(Dynamic objects, exposure, blur 등등)에 의해 기존에 유명한 Open-source Odometry 알고리즘들도 결과가 좋지 않은 것을 볼 수 있다. 이러한 문제들에서 조금 더 Robust하게 Motion Estimation을 하는 방법이 위에서 언급한 Keyframe을 기준으로 뽑는다든가, M-estimator를 적용한다든가 하는 방법인데 센서 단계에서 쉽게 적용할 수 있는 방법이 바로 IMU(Inertial Measurement Unit)를 사용하는 방법이 될 것이다.